FunctionLAPACKdtrsm

2022年8月23日

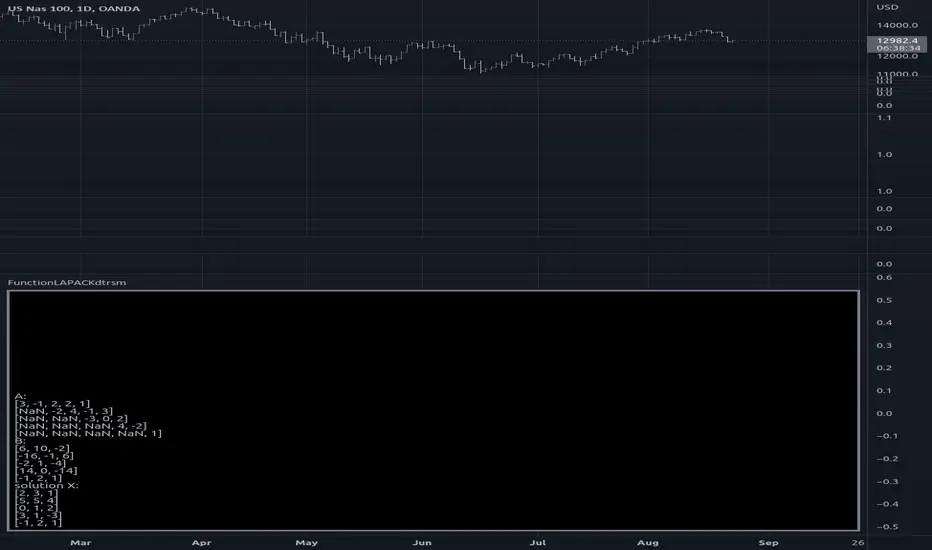
Library "FunctionLAPACKdtrsm"
subroutine in the LAPACK:linear algebra package, used to solve one of the following matrix equations:

op( A )*X = alpha*B, or X*op( A ) = alpha*B,

where alpha is a scalar, X and B are m by n matrices, A is a unit, or
non-unit, upper or lower triangular matrix and op( A ) is one of

op( A ) = A or op( A ) = A**T.

The matrix X is overwritten on B.

reference:
netlib.org/lapack/explore-html/de/da7/dtrsm_8f_source.html

dtrsm(side, uplo, transa, diag, m, n, alpha, a, lda, b, ldb)
  solves one of the matrix equations

op( A )*X = alpha*B, or X*op( A ) = alpha*B,

where alpha is a scalar, X and B are m by n matrices, A is a unit, or
non-unit, upper or lower triangular matrix and op( A ) is one of

op( A ) = A or op( A ) = A**T.

The matrix X is overwritten on B.

  Parameters:
    side: string , On entry, SIDE specifies whether op( A ) appears on the left or right of X as follows:
SIDE = 'L' or 'l' op( A )*X = alpha*B.
SIDE = 'R' or 'r' X*op( A ) = alpha*B.
    uplo: string , specifies whether the matrix A is an upper or lower triangular matrix as follows:
UPLO = 'U' or 'u' A is an upper triangular matrix.
UPLO = 'L' or 'l' A is a lower triangular matrix.
    transa: string , specifies the form of op( A ) to be used in the matrix multiplication as follows:
TRANSA = 'N' or 'n' op( A ) = A.
TRANSA = 'T' or 't' op( A ) = A**T.
TRANSA = 'C' or 'c' op( A ) = A**T.
    diag: string , specifies whether or not A is unit triangular as follows:
DIAG = 'U' or 'u' A is assumed to be unit triangular.
DIAG = 'N' or 'n' A is not assumed to be unit triangular.
    m: int , the number of rows of B. M must be at least zero.
    n: int , the number of columns of B. N must be at least zero.
    alpha: float , specifies the scalar alpha. When alpha is zero then A is not referenced and B need not be set before entry.
    a: matrix<float>, Triangular matrix.
    lda: int , specifies the first dimension of A.
    b: matrix<float>, right-hand side matrix B, and on exit is overwritten by the solution matrix X.
    ldb: int , specifies the first dimension of B.
  Returns: void, modifies matrix b.
usage:
dtrsm ('L', 'U', 'N', 'N', 5, 3, 1.0, a, 7, b, 6)