Fast Fourier Transform [ScorsoneEnterprises]

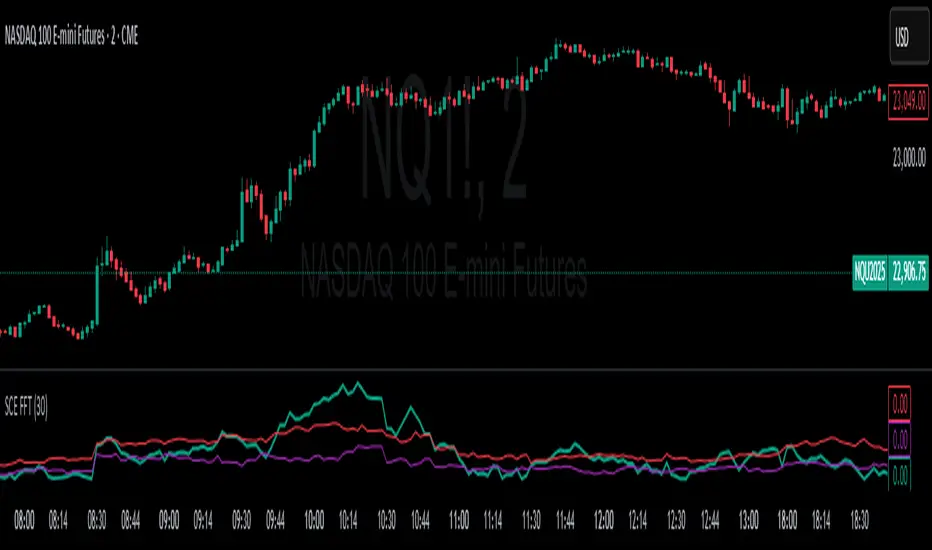
The SCE Fast Fourier Transform (FFT) is a tool designed to analyze periodicities and cyclical structures embedded in price. This is a Fourier analysis to transform price data from the time domain into the frequency domain, showing the rhythmic behaviors that are otherwise invisible on standard charts.

Instead of merely observing raw prices, this implementation applies the FFT on the logarithmic returns of the asset:

Log Return(𝑚) = log⁡(close[𝑚] / close[𝑚+1])

This ensures stationarity and stabilizes variance, making the analysis statistically robust and less influenced by trends or large price swings.

For a user-defined lookback window 𝑁:

Each frequency component 𝑘 is computed by summing real and imaginary projections of log-returns multiplied by complex exponential functions:

𝑒^−𝑖𝜃 = cos⁡(𝜃)−𝑖sin(𝜃)

where:

θ = 2πkm / N

​he result is the magnitude spectrum, calculated as:

Magnitude(𝑘) = sqrt(Real_Sum(𝑘)^2 + Imag_Sum(𝑘)^2)

This spectrum represents the strength of oscillations at each frequency over the lookback period, helping traders identify dominant cycles.

Visual Analysis & Interpretation
To give traders context for the FFT spectrum’s values, this script calculates:

25th Percentile (Purple Line)

Represents relatively low cyclical intensity.

Values below this threshold may signal quiet, noisy, or trendless periods.

75th Percentile (Red Line)

Represents heightened cyclical dominance.

Values above this threshold may indicate significant periodic activity and potential trend formation or rhythm in price action.

The FFT magnitude of the lowest frequency component (index 0) is plotted directly on the chart in teal. Observing how this signal fluctuates relative to its percentile bands provides a dynamic measure of cyclical market activity.

Chart examples



In this CL chart, we see the regime of the price accurately described in the spectral analysis. We see the price above the 75th percentile continue to trend higher until it breaks back below.



In long trending markets like PL has been, it can give a very good explanation of the strength. There was confidence to not switch regimes as we never crossed below the 75th percentile early in the move.



The script is also usable on the lower timeframes. There is no difference in the usability from the different timeframes.

Script Parameters

Lookback Value (N)
Default: 30

Defines how many bars of data to analyze. Larger N captures longer-term cycles but may smooth out shorter-term oscillations.